Another Roasting the Leetcode of the Day: Hand of Straights
Today’s Leetcode is: 846. Hand of Straights (https://leetcode.com/problems/hand-of-straights/)
The general idea is extremely simple: given a list of numbers, divide the numbers equally into multiple lists with k size, where each elements are consecutive numbers. For example: List [1,2,3,6,2,3,4,7,8], divided into list of 3 elements will be: [1,2,3],[2,3,4],[6,7,8]. Make a function to check IF we can make such list or not.
I am checking the provided solution by Leetcode, and oh boy, another bloatware and overly complex way of thinking. Let’s dive in.
Simple Checking
Let’s establish the simplest case here. We can first check if we can construct list if the size of the input list is divisible by k. Otherwise, it is impossible to create the list with that configuration and we can just simply return false. On the other hand, if k equals to 1, it will always be possible to create such list, hence always return true. We only need to process if the input list size is divisible by k and k is not 1.
Leetcode Solution 1: Using Map
Oh my my. Map is an expensive data structure. Their idea was to create a map to store the count of each card value from the input list, then process the map until the map is empty by:
- Get the smallest value from the map
- Iterate the map to check if the consecutive value is available, greedily return false if it cannot find the next consecutive value
- If it can complete everything, return true
From the algorithm itself we can already see multiple issue: using (ordered) map takes longer time as seek operation costs O(log n). But let’s check the code to see even more pain.
The first ick is the insertion. Leetcode claimed that populating the map takes O(n) time. While it is true in case of there is only a single distinct value in the input list. If all values are distinct, then it will take O(n log n) to insert as insertion to an ordered map requires O(log n) and there are n elements, hence O(n log n).
map<int, int> cardCount;
for (int i = 0; i < handSize; i++) {
cardCount[hand[i]]++;
}
The second disaster comes in this processing loop:
// Process the cards until the map is empty
while (!cardCount.empty()) {
// Get the smallest card value
int currentCard = cardCount.begin()->first;
// Check each consecutive sequence of groupSize cards
for (int i = 0; i < groupSize; i++) {
// If a card is missing or has exhausted its occurrences
if (cardCount[currentCard + i] == 0) {
return false;
}
cardCount[currentCard + i]--;
if (cardCount[currentCard + i] < 1) {
// Remove the card value if its occurrences are exhausted
cardCount.erase(currentCard + i);
}
}
}
return true;
The loop perform access on EVERY elements of the map. Accessing map also requires O(log n) as the underlying data structure of the map is a (balanced) tree, hence indexing the map will require O(log n). And what makes it worse is that it USES INDEXING OPERATOR TO ACCESS THE MAP. This results in INSERTING A NEW ELEMENT TO THE MAP ON EVERY INDEXING. Although it may only be performed once as the algorithm returns directly when this branch is taken, this is a BAD programming practice as insertion may trigger tree balancing operation, which is not constant time. Not to mention if the insertion triggers a new allocation, which is unnecessary.
Leetcode Solution 2: Sorting, But Use Map again…
But now use Unordered Map. Again, do counting of all the card, put into map, then iterate the map to check if we can form a sequence of k number. Check their implementation below:
bool isNStraightHand(vector<int>& hand, int groupSize) {
if (hand.size() % groupSize != 0) {
return false;
}
// Map to store the count of each card value
unordered_map<int, int> cardCount;
for (int card : hand) {
cardCount[card]++;
}
for (int card : hand) {
int startCard = card;
// Find the start of the potential straight sequence
while (cardCount[startCard - 1]) {
startCard--;
}
// Process the sequence starting from startCard
while (startCard <= card) {
while (cardCount[startCard]) {
// Check if we can form a consecutive sequence of
// groupSize cards
for (int nextCard = startCard;
nextCard < startCard + groupSize; nextCard++) {
if (!cardCount[nextCard]) {
return false;
}
cardCount[nextCard]--;
}
}
startCard++;
}
}
return true;
}
There are 4-depth nested loop! The mechanism is not so obvious at the first glance, but here’s what I can understand from this approach:
- Find a potential “start number” by looping the number map with decrementing index. It tries to reach into the lowest number from the list which it will be possible to build a sequence
- When finding the potential start number, iterate as many as the maximum k number. If it is not possible, then return false
- Loop until all card is processed
This trick is technically correct and able to have linear time complexity O(n). It avoids in involving sorting algorithm which can give O(n log n) complexity. However, the nested loop makes it hard to read and possibly to debug.
And the main problem again: ACCESSING THE MAP WITH OPERATOR INDEX. Again, it will create UNNECESSARY INSERTION. Just avoid this BAD programming practice. Using find method is way preferable especially in the case that we are unsure if the element is exist. See this discussion in Stack Overflow: https://stackoverflow.com/questions/8800770/why-is-stdmapoperator-considered-bad-practice
How I did
It is simple: Sort the list, then build the sequence, helped by priority queue. If we cannot satisfy building a single sequence, return false directly. If we can complete building the sequence, then return true.
First, I create a helper class called Group. This represents the sequence list. We do not need to store the entire actual list. We just need to store the begin value and end value. The element count is the difference of begin and end plus 1. We want to use this Group object as an element of a priority queue, where the Group with smallest end value is prioritized. So, we also overload the operator less (<) to make it work. Note that priority queue priorities larger element, so in this case, we flip the semantic of the less operator we overload. I also created a helper function appendable, which indicates if we can append a new element to this list or not.
struct Group
{
int begin;
int end;
Group(int c) : begin(c), end(c) { }
int count() const
{
return end - begin + 1;
}
bool appendable(int c, int max) const
{
return count() < max && c == (end + 1);
}
bool operator<(Group const& that) const
{
return that.end < end;
}
};
To process the list, we iterate the sorted list, and check our priority queue. If there’s an element in the priority queue, check if we can append to the top element in the priority queue. If we can, pop the top group, append the element by modifying its end field, and reinsert back to the priority queue if the count is still below the group count. If there is no group in the queue or we cannot append and we can still make a new group, append a new group to the queue. Otherwise, it is failed and we just simply return false.
bool isNStraightHand(std::vector<int>& hand, int groupSize)
{
return hand.size() % groupSize == 0 && (groupSize == 1 || [&] () {
std::ranges::sort(hand);
std::priority_queue<Group> groups;
int groupCount = hand.size() / groupSize;
for(int card : hand)
{
if(!groups.empty() && groups.top().appendable(card, groupSize))
{
Group top = groups.top();
groups.pop();
top.end = card;
if(top.count() < groupSize)
groups.push(top);
else
groupCount--;
}
else if(groups.size() < groupCount)
groups.emplace(card);
else
return false;
}
return true;
}());
}
My implementation does not use any map. Only helped by a priority queue, which is backed by a heap that may not also cost a lot of space. Despite the complexity can reach O(n log n), in Leetcode, I easily beat 100%, reaching 14ms in time, and beats 96% by using only 24 MB of memory.
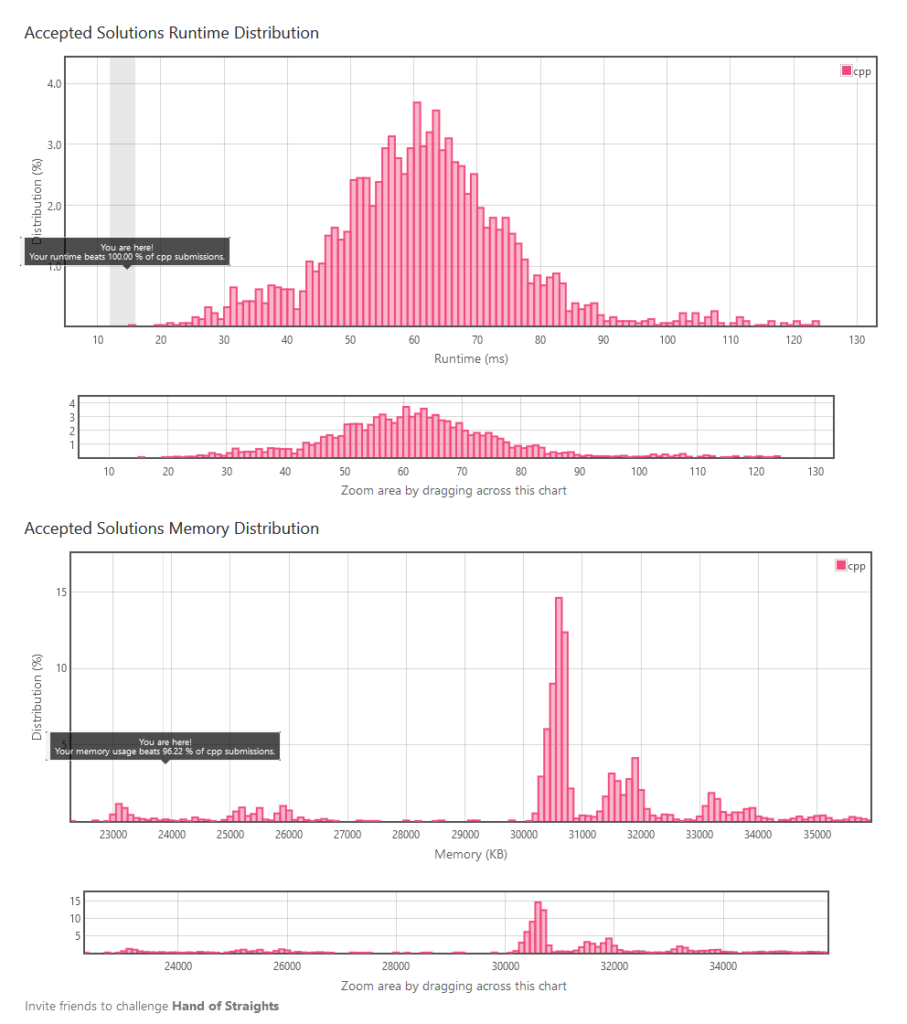
My key takeaway is: think simpler, choose your data structure wisely, and AVOID USING BAD PRACTICE SUCH AS ACCESSING CONTAINERS WITH OPERATOR INDEX.
Painful Takes
Before we wrap up, let’s see some painful codes submitted in this challenge!
It is using priority queue as well, but why the handwritten template? I know that priority queue template definition is not the best design decision (why they put the Compare type after the Container type; people don’t typically care about the container, rather want to implement custom comparer instead). But the thing is that this implementation wants to store two integer similar to my implementation, but they do not want to write a new class for this. This is also a BAD practice. Write a new class to have clearer semantic of data you are trying to store. std::pair should only be used if the value represented in the pair is obvious enough. Two pair of integers stored in a priority queue is not obvious at all and makes the code hard to read. I avoid all this by making a separate class, and implement operator overloading correctly so the priority queue can just use the default template instantiation. Using std::pair does not give performance benefit at all compared to writing your own class.
class Solution {
public:
bool isNStraightHand(vector<int>& hand, int groupSize) {
if(hand.size()%groupSize != 0){
return false;
}
map<int,int> mp;
for(int i=0; i<hand.size(); i++){
mp[hand[i]]++;
}
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> pq;
for(auto i:mp){
pq.push({i.first,i.second});
}
int prevElem;
while(!pq.empty()){
vector<pair<int,int>> temp;
for(int i=0; i<groupSize; i++){
int val = pq.top().first;
int f = pq.top().second;
f = f-1;
pq.pop();
if(i>0 && (val - prevElem != 1)){
return false;
}
prevElem = val;
cout<<prevElem<<" ";
temp.push_back({val,f});
}
for(auto i:temp){
if(i.second>0){
pq.push({i.first,i.second});
}
}
}
return true;
}
};
class Solution {
public:
bool isNStraightHand(vector<int>& hand, int k) {
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> p,q;
unordered_map<int,int> m;
for(int x:hand) m[x]++;
for(auto x:m) q.push(x);
while(!q.empty()){
for(int i=1;i<k;i++){
auto x = q.top();
q.pop();
if(q.empty() || x.first+1 != q.top().first) return false;
x.second--;
if(x.second) p.push(x);
}
auto x = q.top();
q.pop();
x.second--;
if(x.second) p.push(x);
while(!p.empty()){
q.push(p.top());
p.pop();
}
}
return true;
}
};
Certainly a lot of people does not code C++ cleanly and has to be trained more.

